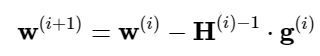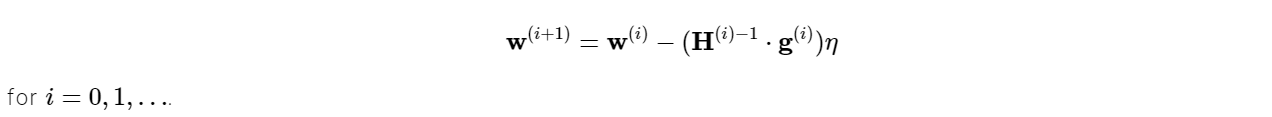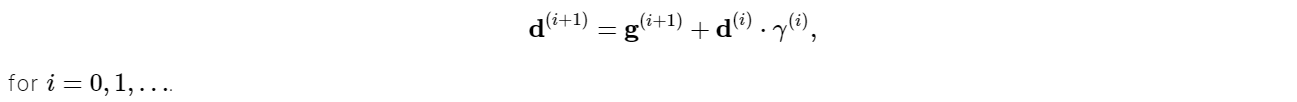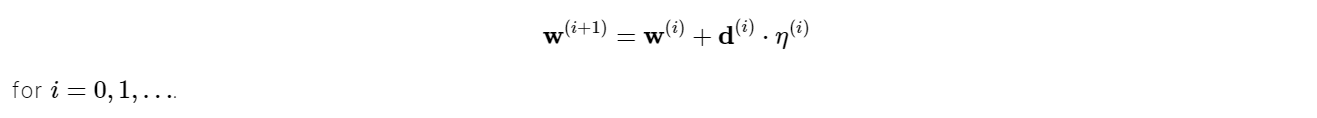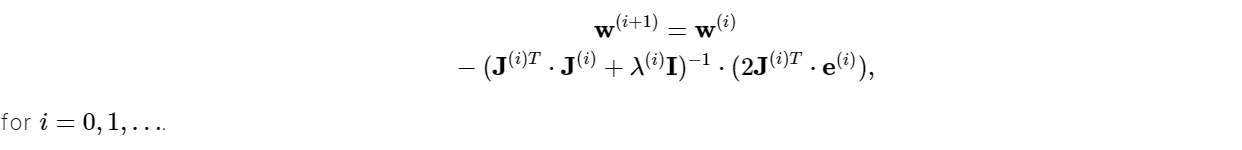ANN Training Algorithms
Algorithms called artificial neural networks mimic how the central nervous system operates. Artificial neural networks come in a variety of forms. Such systems are constructed using a set of values and computational procedures that affect the output.
ANN Architecture
An artificial neural network is modelled after the human nervous system. Its components can be grouped into three distinctive layers:
Input Layer
It is the first layer in any network. No model can function without proper input. As the name implies, it handles inputs in various forms specified by the developer.
Hidden Layer
The hidden layer appears here between the input and output level. It runs all of the computations to uncover hidden characteristics and trends.
Output Layer
The data provided as input goes through a sequence of changes with the hidden layer, resulting in an output communicated to the developer at this level.
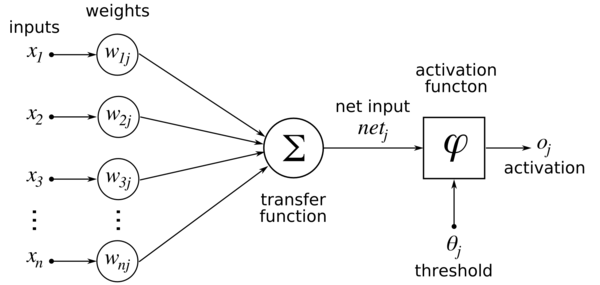
The artificial neural network accepts data from the input layer and calculates the weighted total of the inputs and bias. A mathematical formula known as a transfer function is used to express this calculation. First, it calculates the weighted total, which is fed into an activation function to generate the result. Activation functions decides whether or not a node should trigger. The triggered nodes are the only ones that get to the output nodes. Several activation functions can be used depending on the type of project we are undertaking.
An example of this process and the calculations involved are explained in the diagram shown below:
Working of Artificial Neural network
There are 3 or more linked layers in an artificial neural network. Nerve cells in the input layer make up the very first layer. These neurons transmit information to greater depths and then transmit the ultimate output information to the output level.
The units that make up the concealed inner layers flexibly alter the data sent from layer to layer. Every layer functions has both input and output, enabling the ANN to comprehend increasingly intricate things. The neural layer is the catchall term for these inner layers.
By weighing the collected data according to the ANN’s internal logic, the cells in the neural layer try to understand the data.
How to train your ANN?
To train an artificial neural network, one must select from a set of permitted models where each model has several corresponding methods.
One of the best benefits of an ANN is that it can train by viewing large datasets. An ANN offers several other benefits as well. In this approach, ANN acts as a means for approximating random functions. When establishing complex calculations or distribution patterns, these techniques can predict the most perfect and economical ways to arrive at answers.
To find answers, ANN uses data sampling instead of whole data sets, which minimises both time & expense. ANNs are thought of as relatively straightforward statistical methods of improving current data analysis technology.
Learning techniques for an ANN:
Supervised Learning:
Throughout this learning process, the structure is fed with training data. Since the intended output is already established, parameters are modified until the required value is produced.
Unsupervised Learning:
Train the model whose result is predictable using the input data. By extracting features from the incoming data, the network classifies the data and modifies the weights.
Reinforcement Learning:
The system here offers feedback on whether the result is correct or incorrect, although the output is uncertain. It is learning under partial supervision, where the output is overseen, and feedback is provided based on its accuracy.
Offline Learning:
The weight matrix and threshold are adjusted after the network has seen the training dataset. Another name for it is batch learning.
Online Learning:
Following the presentation of every training instance to the system, the weights and threshold are adjusted.
Training algorithms for ANN:
Gradient Descent
In the event of a supervised training situation with an ANN, this is the most basic training algorithm employed. First, the mistake or discrepancy is identified if the measured output deviates from the desired output. Then, the network’s weights are adjusted via the gradient descent technique to reduce this error.
Back Propagation
It is a development of the delta learning rule based on gradients. Here, the mistake is communicated backwards from the output layer to an input layer through the hidden layer after being discovered (the discrepancy between the intended and target). It is employed in the context of multilayer neural networks.
Backpropagation is a technique used by an extra set of learning rules that allows the ANN to correct its output results by considering mistakes. The data is transmitted backwards by backpropagation each time the output is classified as a mistake in the supervised training stage. Every value is adjusted according to how significantly it contributed to the inaccuracy.
Newton’s method
Since it employs the Hessian matrix, Newton’s approach is a second-order procedure. This strategy aims to develop superior training pathways by utilising the second derivatives of the loss function. As a result, Newton’s method evolves as follows, beginning with a parameter vector w(i).
This is known as Newton’s step. It should be noted that this parameter adjustment may result in a maximum instead of a minimum if the Hessian matrix is not positively definite. As a result, Newton’s technique does not ensure that the loss index will be reduced at each repetition. To avoid this, Newton’s method formula is frequently adjusted as follows:
The training rate η can be either preset or determined through line minimisation. Nevertheless, Newton’s technique has the disadvantage that the correct assessment of the Hessian and its inverse is computationally intensive.
Conjugate Gradient
The conjugate gradient method is a middle ground between gradient descent and Newton’s technique. It is driven by the need to speed up the normally slow convergence related to gradient descent. This method also eliminates the data needs involved with storing, evaluating, and inverting the Hessian matrix, as Newton’s method does.
The search is carried out alongside conjugate directions in this training process. As a result, it produces faster convergence than gradient descent directions generally.
Let us designate the training direction vector by d and represent the method mathematically as follows:
γ is the conjugate factor, and it can be calculated in a variety of methods. Fletcher and Reeves and Polak and Ribiere are the most commonly used methods. The training direction is regularly adjusted to the gradient’s negative in all these conjugate gradient methods. The parameters are then adjusted to improve the process using the formula below.
The parameters are then adjusted to improve the process using the formula below. Line minimisation is commonly used to determine the training rate, η.
Levenberg-Marquardt
The Levenberg-Marquardt algorithm is specially created for use with loss functions composed of a sum of squared errors. Moreover, it is designed for functions of the sum-of-squared-error kind. This makes it particularly quick to train neural networks based on such errors.
The parameter λ is set to a big value to ensure that the first iterations are small steps in the gradient descent axis. If any cycle fails, then it is incremented by some amount. Otherwise, when λ diminishes, it is lowered, bringing the Levenberg-Marquardt algorithm closer to the Newton technique. This procedure usually speeds up the convergence to minimum. This approach, though, has certain limitations.
For starters, it cannot minimise functions like root mean squared error or cross-entropy error. Furthermore, with huge amounts of data and neural networks, the Jacobian matrix grows massive, necessitating a substantial amount of memory. As a result, when dealing with large data sets or neural networks, the Levenberg-Marquardt approach is not recommended.
Conclusion
Artificial neural networks have a broad range of beneficial uses, including chatbot computational linguistics, spam email identification, and prescriptive analytics in data analytics, among others. But it is necessary to know how to train a network before we can apply it to real-world problems, which is what this article aims to shed light on.