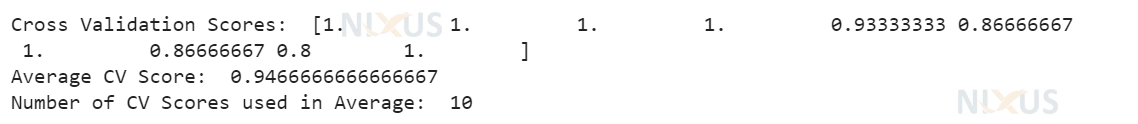Cross Validation in Machine Learning
Any ML model must reliably anticipate the correct result from various input values in various datasets. Stability is the term used to describe this property of a machine learning model. When a model does not significantly alter when its input is changed, it has been trained successfully to generalize and identify patterns in our data.
A crucial phase in a data science project’s developmental process is model development. Depending on the type of problem, we try to use different supervised or unsupervised ML models to train our data set.
How can one be sure that the model is working correctly? Has the model been appropriately trained? All of this can be established by observing how it functions on previously unknown data that it has never seen before. It must be ensured that the model’s accuracy remains consistent throughout. To put it another way, one must validate the model.
One may test the accuracy of our model with the help of cross-validation in ML.
Cross-Validation
A cross-validation is an ML approach used to train and test the model on a subset of the database, then divide it into new subsets and test it again. This implies that we divide our dataset into many segments, train on some of them, and then use the remaining portions for testing rather than breaking it into two parts, one for training and the other for testing. We then use a different section to develop and evaluate our model. This guarantees that our model is being trained and tested on fresh data at each new step.
Although many distinct Cross-Validation strategies exist, let’s first examine their fundamental operation.
1. Set aside a portion of the dataset as a validation set.
2. Utilize the training dataset to train the model.
3. Employing the validation set, assess the model’s performance. Perform the next step if the model’s performance comes out to be good with the validation set; otherwise, look for problems.
Different cross-validation techniques
You may already be aware of the several cross-validation strategies. While some are frequently employed, others simply function in theory. Here are some examples of the cross-validation techniques that will be discussed.
1. Holdout Method
2. K-Fold Cross-validation
3. Leave-P-Out Cross-validation
4. Leave-one-out Cross-validation
5. Stratified K-Fold Cross-validation
6. Time series cross-validation
Holdout Method
The most common and most popular method is hold-out cross-validation. You utilize the hold-out technique daily, even if you are unaware.
The hold-out technique’s algorithm:
1. The training and test sets should be separated from the dataset. Usually, 20% of the dataset is used as the test set and 80% as the training set, but you can choose any other division that works better for you.
2. On the training set, train the model.
3. Verify with the test set.
4. Save the validation’s outcome.
K-Fold Cross-validation
One strategy to enhance the holdout method is K-fold cross-validation. This approach ensures that our model’s score is independent of how we chose the training and testing sets. The data set is partitioned into k subsets, and the holdout procedure is performed k times. Let’s take it one step at a time:
1. Divide your dataset into k folds (subsets) at random.
2. Build your model on k – 1 folds of your dataset for each fold.
3. The model should then be tested to see how effective it is for the kth fold.
4. Repeat this process until all k-folds have worked as the testing set.
5. The cross-validation accuracy is the average of k recorded accuracy and will serve as the model’s performance statistic.
This strategy produces a less biased model than other methods since it assures that every finding from the initial data set can appear in both the training and test sets. This is one of the most effective methods if we just have a small amount of input data.
Leave-P-Out Cross-validation
When we use this exhaustive procedure, we remove p points from all the data points in the dataset (say x). We train the model on these (x – p) data points and test it on these t data points. This technique is repeated for all possible p combinations in the original dataset. The ultimate accuracy is obtained by averaging the accuracies from all iterations.
This strategy is exhaustive since the model’s training is done on all the potential combinations of data points. Remember that if we choose a more significant value for p, the number of combinations increases, and we may say the approach becomes much more exhaustive.
Leave-one-out Cross-validation
This is a basic variant of Leave-P-Out cross-validation, with p set to one. This reduces the method’s exhaustiveness because we now have x choices for x data points and p = 1.
Stratified K-Fold Cross-validation
It can be challenging to use K Fold on a classification task. Because we’re shuffling the data randomly and subsequently splitting it into folds, we may end up with severely disproportionate folds, causing our training to be biased. For example, suppose we have a fold with a majority of one class (say, “TRUE”) and only a few in the “FALSE” class. This will almost probably disrupt our training; therefore, we will use stratification to create stratified folds.
The data is rearranged through the stratification process to ensure that every fold provides a good representation of the whole. It is desirable to arrange the data to ensure each category makes up approximately fifty per cent of the instances in each fold, for example, in a binary classification task where each class contains 50% of the data.
Example of Cross-Validation
Below is an example in Python: averaging the results across all folds; it is also an excellent strategy to examine how the cross-validation did overall.
from sklearn import datasets
from sklearn.ensemble import RandomForestClassifier
import pandas as pd
from sklearn.model_selection import KFold, cross_val_score
X, y = datasets.load_iris(return_X_y=True)
Nixus_clf = RandomForestClassifier(random_state=42)
k_folds = KFold(n_splits = 10)
scores = cross_val_score(Nixus_clf, X, y, cv = k_folds)
print("Cross Validation Scores: ", scores)
print("Average CV Score: ", scores.mean())
print("Number of CV Scores used in Average: ", len(scores))
Output
Note that it is entirely over your model and how exactly it is doing with different settings or parameter values that you are using. Therefore, if your model doesn’t meet your criteria after you’ve cross-validated the models, you can change the parameter values for the next model.
Cross-Validation Vs. Train & Test Split
| Train & Test Split | Cross- Validation |
| Less Efficient as in Train/Test split, training set performs the task of training the data and testing dataset performs testing only. | More Efficient as each observation goes through both train and test split |
| The train set performs training per the split ratio (e.g. 80:20, 85:15, etc.) and then goes for testing. This type of splitting causes more variance leading to a less effective model. | CV overcomes the issue of high variance by further dividing the whole dataset into groups of training and testing sets and then taking an average of the output. |
| Once we have trained our model for, say, 70% of the aspect ratio, then testing of the model can only be done for the remaining ratio, and one has to settle for those findings only | The model can be optimized anytime by using the training set to get a more desirable performance. |
Benefits of Cross-validation
1. As the name suggests, cross-validation validates the dataset by cross-checking all the combinations, which is done with the help of folds. To do this, the dataset is split into many folds. Then the model is sent for training over these folds. With this, the algorithm doesn’t undergo overfitting issues during training. Hence, our model gains the capability of generalizing, which is a good sign of a resilient model.
2. To make the algorithm more effective, cross-validation aids in determining the ideal value for the hyperparameters, also known as hyperparameter tuning.
Drawbacks of Cross-validation
1. The duration of training is significantly extended by cross-validation. Previously, you could only use one training set to train your model; now, you must use several training sets to do cross-validation.
2. The processing power needed for cross-validation is quite expensive computationally.
Different Cross-validation applications
1. This method may be employed to evaluate how well various predictive modelling approaches work.
2. It has much potential for different areas such as healthcare, agriculture, finance, transport, etc.
3. As data scientists are already using it in the field of medical statistics and also being used in the agriculture field, it can also be utilized for meta-analysis.
Conclusion
During the model-building process, paying close attention to the algorithm’s generalisation capabilities is an essential task, and to do so, cross-validation becomes an effective technique. It needs to be well-known to every data scientist. In reality, one needs to cross-validate a model to complete the project.