K-Means Clustering in Machine Learning

In past articles, we have spoken in length about machine learning, its types and some algorithms. In this article, we are going to delve deep into one of the most popular clustering algorithms: K-Means clustering. Let’s start!!

What is K Means Clustering?

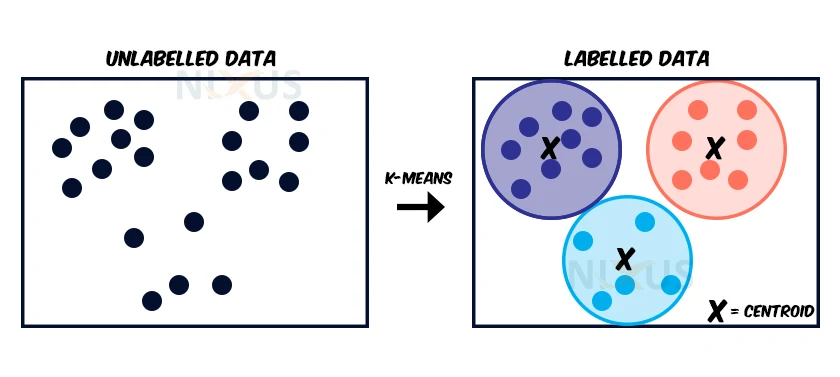
K-Means Clustering is a clustering technique that falls int the unsupervised learning part of things. It works by dividing a dataset (data without labels) into clusters. K is the number of predefined clusters that the operation produces.

It is an iterative technique that splits the unlabeled dataset into k distinct clusters, with each dataset belonging to just one group with identical attributes. It enables us to cluster the data into distinct groups and provides a quick method for discovering the categories of groups in an unlabeled dataset without the requirement for training.

This is a centroid-based technique, with each cluster having its own centroid. The goal of this approach is to minimize the sum of distances between data points and their associated clusters.

Working of K Means Clustering

You’ll specify a goal number k, which represents the number of centroids required in the dataset. A centroid is an imagined or actual point that represents the cluster’s centre.

You map each data point to one of the clusters by lowering the in-cluster sum of squares.

In other words, the K-means algorithm finds k centroids and then assigns every data point to the closest cluster while keeping the centroids as small as feasible.

The ‘means’ in K-means refers to data averaging; that is, determining the centroid.

Choosing number of clusters:

The K-means clustering algorithm’s success is dependent on the very effective groups it creates. However, determining the ideal number of clusters is a difficult process. There are other methods for determining the best number of clusters, but we will focus on the most efficient methodology for determining K value. The procedure is as follows:

Among the most prominent methods for determining the appropriate number of clusters is the Elbow method. This approach makes use of the WCSS value notion. Within Cluster Sum of Squares (WCSS) is a term that describes the total variances within a cluster. The equation for determining the WCSS value (for three clusters) is as follows:

Elbow method working:

One can choose any approach, such as Euclidean distance or Manhattan distance, to measure distances between pieces of data and the centroid.

The elbow technique uses the procedures below to get the best cluster value:

• It performs K-means clustering on a dataset for various K values (ranges from 1-10).
• Determines the WCSS value for every K.
• Plot showing a curve between both the number of clusters K and the estimated WCSS values.
• When a severe bend resembles an elbow, that location is regarded the optimal K value.

Because the plot depicts a steep bend that resembles an elbow, it is referred to as the elbow technique.

Applications of K Means Clustering

1. Customer Segmentation:

Fulfilling customers’ demands is the beginning point for relationship marketing, and realising that no two consumers are alike, and that the same offers may not work for all, we can enhance the process. We can however, segment clients based on their requirements and habits, which can assist businesses in marketing their products to the correct customers. For example, telecom businesses have a big number of users, and by employing market or customer segmentation, they may customise marketing and incentives, among other things.

2. Fraud detection:

The ongoing expansion of the internet and online services is increasing security concerns. Accounting for these security issues or fraudulent behaviors, such as logging into an Instagram account from an odd city or concealing any type of financial misdeed, is common nowadays.

Using techniques like K-means Clustering, it is simple to find patterns in any unexpected activity. The presence of an outlier indicates the presence of a fraud occurrence.

3. Document classification:

K-Means is recognised for being efficient in the case of huge datasets, which makes it one of the best alternatives for document classification. Documents are put into different categories depending on their subjects, content, and tags, if any are provided. The files will be converted to vector format. Then, we utilise word frequency to discover common terms, and from there, we may identify commonalities between document groupings.

Advantages of K Means Clustering

Some of the benefits of K-Means clustering techniques are as follows:

• It is simple to comprehend and execute.
• K-means would be quicker than Hierarchical clustering if we had a high range of parameters.
• An example can modify the cluster when centroids are recalculated.
• When opposed to Hierarchical clustering, K-means produces smaller groupings.

Disadvantages of K Means Clustering

A few of the drawbacks of K-Means clustering techniques are as follows:

• The batch size, or the value k, is tough to estimate
• Starting inputs such as the number of clusters have a significant influence on outcome
• The sequence in which the information is stored will have a significant influence on the final result.
• It is quite prone to rescaling. If we use normalisation or standards to rescale our data, the result will be drastically different.

Summary

K-means clustering is a popular approach for data cluster analysis. It is simple to grasp, especially if you use a K-means clustering lesson to speed up your understanding. It also produces training outcomes rapidly. However, because minor alterations in the data might lead to high variance, its efficiency is typically not as competitive as that of other complex clustering approaches.